

However, the efficient market hypothesis says that major investors have access to the same information and form the same subjective probability distributions based on this information. But is the market really efficient? Since CAPM is a consequence of this hypothesis, we could see if historical data contradict CAPM, which would thereby contradict the efficient market hypothesis. The efficient market hypothesis is reasonable and leads eloquently to CAPM. (Note that Least Squares may equivalently be called Least Mean of Squares.) The Least Median of Squares (LMS) estimator, suggested by Rousseeuw (1984), ranks highly in this regard, as its breakdown point is 50%. The breakdown point of an estimator is the smallest percentage of outliers that may cause the estimator to be affected by a bias. Among possible regression criteria, high breakdown point estimators are often regarded as desirable. Alternatively, the use of robust or resistant estimation methods to obtain the regression parameters has been proposed ( Chan and Lakonishok, 1992, Martin and Simin, 2003). Some earlier contributions in the finance literature suggested some form of shrinkage of extreme β estimates towards more reasonable levels, with different theoretical justifications (see for example Blume, 1971, or Vasicek, 1973).
Capital asset pricing model series#
Least Squares has appealing theoretical and practical (numerical) properties, but obtained estimates are often unstable in the presence of extreme observations which are common in financial time series ( Chan and Lakonishok, 1992 Knez and Ready, 1997 Genton and Ronchetti, 2008). The standard method to obtain parameter estimates in a linear regression is Least Squares. When we re-interpret the CAPM as a one-factor model ( Luenberger, 1998, Chapter 8), however, the β estimates become useful measures of a stock's general correlation with the market, which may be used to construct variance–covariance matrices ( Chan et al., 1999). Enrico Schumann, in Numerical Methods and Optimization in Finance (Second Edition), 2019 Robust/resistant regressionĮmpirical evidence has shown that the Capital Asset Pricing Model (CAPM) explains asset returns in the cross-section rather poorly ( Fama and French, 1993, 2004). The author is grateful to Steve Shreve for illuminating discussions and information. A natural discretization of the continuous time model introduces a situation of incompleteness. However, the analogue of the continuous time model when the randomness is modelled by a finite number of Wiener processes is not. The situation of a finite number of random events at each period is compatible with an assumption of complete markets. We present here a detailed theory of what can be done in discrete time. In discrete time, although natural, the corresponding treatment is not widely available in the literature (see Shreve for a partial treatment in the case of the binomial model). The theory has been further developed in continuous time, using properties of martingale generated by Wiener processes (see Karatzas and Shreve ). Curiously, this dynamic version is in continuous time and not in discrete time.
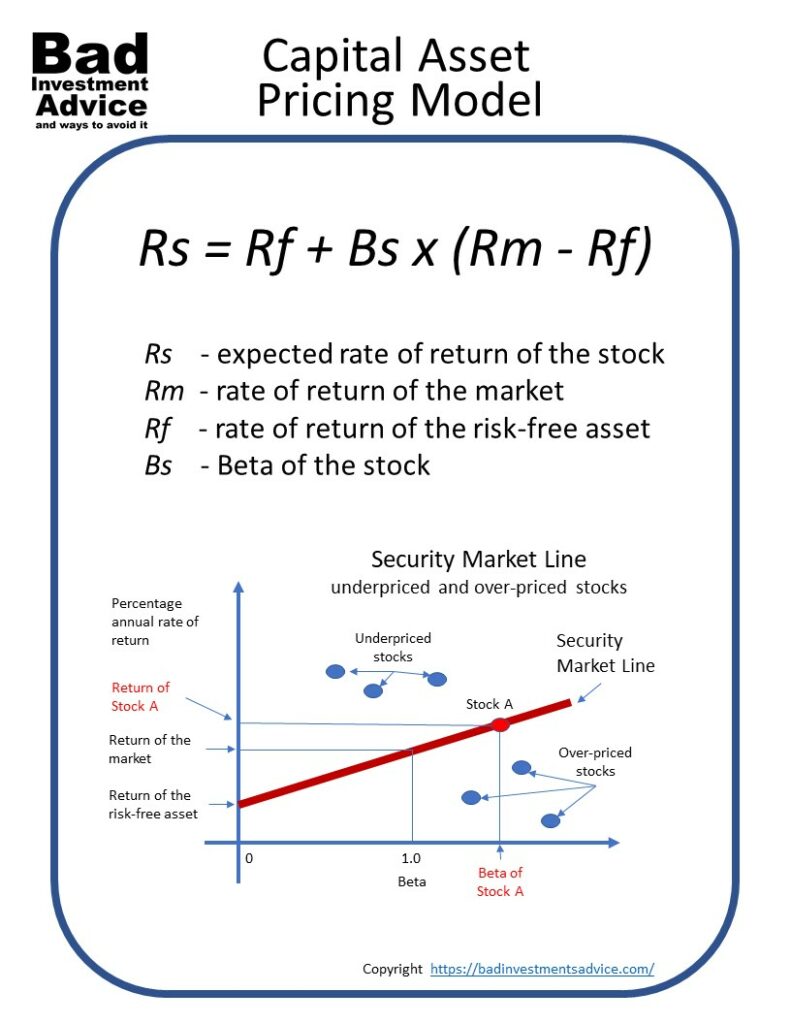
A dynamic version of this model, called the intertemporal capital asset pricing model, has been introduced by Merton. This fact is well known for a single-period problem. When there are only a finite number of states of nature and when the assumption of complete markets is valid, these prices play a significant role in obtaining the optimal consumption and portfolio investment policies in a general setup. The concept of price of state of nature is a concept of stochastic economics introduced by Arrow and Debreu. The capital asset pricing model is a major theory in modern finance. Alain Bensoussan, in Handbook of Numerical Analysis, 2009 1 Introduction


 0 kommentar(er)
0 kommentar(er)
